Gerak harmonik sederhana adalah gerak osilasi yang periodic dan tidak pernah
teredam yang biasanya mengikuti Hukum Hooke (bahwa gaya akan berbanding lurus
dengan perubahan gerak) gerak harmonic secara umum terdiri atas gerak harmonic
sederhana dan gerak harmonic teredam.
Gerak harmonic sederhana adalah gerak periodic dengan lintasan yang ditempuh
selalu sama (tetap). Gerak harmonic sederhana mempunyai persamaan gerak dalam
bentuk sinusoidal dan digunakan untuk menganalisis suatu gerak periodic
tertentu. Gerak periodic adalah gerak berulang atau berosilasi melalui titik
setimbang dalam interval waktu tetap. Gerak harmonic sederhana dapat dibedakan
menjadi dua bagian, yaitu :
a. Gerak harmonic sederhana linier, misalnya penghisap dalam silinder gas,
gerak osilasi air raksa / air dalam pipa U, gerak horizontal atau vertical dalam
pegas, dan sebagainya.
b. Gerak harmonic sederhana angular, misalnya gerak bandul, bandul fisis,
osilasi ayunan torsi, dan sebagainya.
System pegas adalah sebuah pegas dengan konstanta pegas (k) dan diberi massa
pada ujungnya dan diberi simpangan sehingga membentuk gerak harmonic. Gaya yang
berpengaruh pada system pegas adalah gaya Hooke. Gerak harmonic sederhana
disebabkan oleh gaya pemulih atau gaya balik linier (F), yaitu resultan
gaya yang arahnya selalu menuju titik kesetimbangan dan besarnya sebanding
dengan simpangannya, dimana arah gaya selalu berlawanan dengan arah
simpangannya. Sehingga Hukum Hooke :
F = - k x
Dimana :
k = ketetapan gaya/konstanta pegas
x = simpangan (m)
F = gaya pemulih (N)
Pada dasarnya osilasi atau getaran dari pegas yang digantungkan secara
vertikal sama dengan getaran pegas yang diletakan horisontal. Bedanya, pegas
yang digantungkan secara vertikal lebih panjang karena pengaruh gravitasi yang
bekerja pada benda (gravitasi hanya bekerja pada arah vertikal, tidak pada arah
horisontal). Mari kita tinjau lebih jauh getaran pada pegas yang digantungkan
secara vertical.
Pada pegas yang kita letakkan horisontal (mendatar), posisi benda disesuaikan
dengan panjang pegas alami. Pegas akan meregang atau mengerut jika diberikan
gaya luar (ditarik atau ditekan). Pada pegas yang digantungkan vertikal,
gravitasi bekerja pada benda bermassa yang dikaitkan pada ujung pegas.
Akibatnya, walaupun tidak ditarik ke bawah, pegas dengan sendirinya meregang sejauh . Pada
keadaan ini benda yang digantungkan pada pegas berada pada posisi setimbang.
Kita dapat memperhatikan suatu system osilasi terdiri atas satu pegas dengan
konstanta pesas k, dan satu benda bermassa m, yang terletak di
atas bidang datar licin tanpa gesekan, seperti pada gambar a. Benda kita beri
simpangan sedikit ke kanan, kemudian kita lepaskan lagi, sehingga system
berosilasi dengan keadaan umumnya seperti pada gambar b.
Dari Hukum II Newton, maka persamaan gerak untuk massa m dengan
mengabaikan gaya gesekan, adalah :
Berdasarkan hukum II Newton, benda berada dalam keadaan setimbang jika gaya
total = 0. Gaya yang bekerja pada benda yang digantung adalah gaya pegas ( F= -
k x) yang arahnya ke atas dan gaya berat ( W = mg) yang arahnya ke bawah. Total
kedua gaya ini sama dengan nol. Analisis secara matematisnya
Kita akan tetap menggunakan lambang x agar tetap bisa dibandingkan dengan
pegas yang diletakan horisontal. x dapat digantikan dengan y. Resultan gaya yang
bekerja pada titik kesetimbangan = 0. Hal ini berarti benda diam atau tidak
bergerak.
Jika kita meregangkan pegas (menarik pegas ke bawah) sejauh x, maka pada
keadaan ini bekerja gaya pegas yang nilainya lebih besar dari pada gaya berat,
sehingga benda tidak lagi berada pada keadaan setimbang (perhatikan gambar di
bawah).
Pada titik setimbang, besar gaya total = 0, tetapi laju gerak benda bernilai
maksimum (V maks). Pada posisi ini, Ek bernilai maksimum, sedangkan Ep= 0.
Ek maksimum karena V maks, sedangkan Ep= 0, karena benda berada pada titik
setimbang (x=0).
Karena pada posisi setimbang kecepatan gerak benda maksimum, maka benda
bergerak terus ke atas sejauh -x. Laju gerak benda perlahan-lahan menurun,
sedangkan besar gaya pemulih meningkat dan mencapai nilai maksimum pada jarak
-x. Ketika benda berada pada simpangan sejauh -x, Ep bernilai maksimum sedangkan
Ek =0.
Setelah mencapai jarak -x, gaya pemulih pegas menggerakan benda kembali lagi
ke posisi setimbang (lihat gambar di bawah). Demikian seterusnya. Benda akan
bergerak ke bawah dan ke atas secara periodik. Selama benda bergerak, selalu
terjadi perubahan energi antara Ep dan Ek. Energi Mekanik bernilai tetap. Saat
benda berada pada titik kesetimbangan (x = 0), EM=Ek. Ketika benda berada pada
simpangan sejauh -x atau +x, EM = Ep.
Energi Potensial sebuah pegas dengan konstanta gaya k yang teregang sejauh x
dari kesetimbangannya dinyatakan dengan persamaan :
Ep = ½ k
Energi Kinetik sebuah benda bermassa m yang bergerak dengan kelajuan v
ialah :
Ek = ½ m
Energi total (Energi Mekanik) adalah jumlah Energi Potensial dan Energi
Kinetik :
Ketika benda berada pada posisi kesetimbangan, benda memiliki kecepatan
maksimum, sedangkan besar simpangan = 0 (x = A = 0). Dengan demikian pada
titik kesetimbangan, total Energi Mekanik benda yang berosilasi pada ujung pegas
adalah :
EM = Ep+Ek
EM = ½ k(0) +½ mv
EM = ½ mv
Ketika benda berada pada simpangan maksimum, x = A (A = Amplitudo),
kecepatan benda = 0, sehingga Energi Mekanik benda :
EM = ½ kA²
Persamaan ini memberikan sifat umum penting yang dimiliki Gerak Harmonik
Sederhana (GHS)
“ Energi total pada Gerak Harmonik Sederhana berbanding lurus dengan
kuadrat amplitudo.”:
Jika kita menyimpangkan sebuah benda dari kesetimbangan dan melepaskan, maka
benda itu akan berosilasi bolak-balik di sekitar kedudukan setimbang. Waktu bagi
benda untuk melakukan satu osilasi penuh disebut periode T. Sedangkan periode f
adalah banyaknya osilasi tiap detik.
Dalam getaran pegas dapat digunakan satu buah pegas atau beberapa buah pegas
dengan berbagai posisi gabungan, misalnya terhubung seri, paralel atau gabungan
seri dan paralel.
Tetapan konstanta pegas total (gabungan) untuk hubungan seri adalah :
Tetapan konstanta pegas total untuk hubungan paralel adalah :
Sehingga kita tahu bahwa gaya yang bekerja pada pegas yang disusun secara
paralel adalah:
F= -(K1 +K2)X
Dengan X adalah panjang masing-masing pegas dalam keadaan setimbang. Dari
Hukum II Newton, dapat kita tuliskan sebagai berikut :
Dengan F adalah gaya yang terjadi pada pegas, k adalah konstanta pegas dan x
adalah simpangan getaran pegas.
Percepatan gravitasi dapat ditentukan dengan persamaan :
Dimana :
k = konstanta pegas
m = massa beban (kg)
xa = simpangan (m)
t = waktu (s)
a = percepatan gravitasi (m/s2)
Solusi dari persamaan getaran umum adalah :
Dan








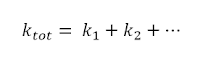




0 Response to "GETARAN TERGANDENG"
Post a Comment